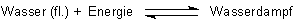
Freie Energie und Temperatur. Die Gibbs-Helmholtz-Gleichung
Zwei auf den ersten Blick konträre Naturgesetze bewirken Veränderungen in einem System.
Naturgesetz 1:
Die Natur ist bestrebt, den energieärmsten Zustand
einzunehmen
Naturgesetz 2:
Die Natur ist bestrebt, den Zustand größtmöglicher
Unordnung einzunehmen
Den Energiezustand beschreibt man im Allgemeinen mit der Zustandsgröße Enthalpie (Symbol H), den Unordnungszustand mit der Entropie (Symbol S).
Das Gegeneinanderwirken dieser beiden Zustandsgrößen lässt sich am besten am Verdampfen einer Flüssigkeit zeigen.
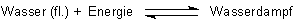
Das von uns untersuchte System besteht aus Flüssigkeit und Dampfraum.
Aktion 1: Wasser (fl.) + Energie ———> Wasserdampf
Wir führen dem System laufend Energie in Form von Wärme zu. Dadurch wird der Energiegehalt
des Systems ständig erhöht. Das widerspricht dem ersten "Naturgesetz".
Die Flüssigkeit verdampft, in dem die Moleküle sich stärker bewegen und am Siedepunkt in den
Dampfzustand übergehen. Das bedeutet eine starke Zunahme an Unordnung. Hier stimmt die Aussage
des zweiten "Naturgesetzes".
Aktion 2: Wasserdampf ———>
Wasser (fl.) + Energie
Lässt man das System wieder abkühlen, so entzieht man dem System Energie; d. h., die Enthalpie
nimmt ab. Hier stimmt die Aussage des ersten "Naturgesetzes".
Ein Teil des Dampfes kondensiert. Das hat zur Folge, dass die Unordnung im System geringer
wird. Das bedeutet eine Verminderung der Entropie und widerspricht dem zweiten "Naturgesetz".
Diese Überlegungen haben dazu geführt, den jeweiligen Zustand des Systems anhand einer neuen Zustandsgröße zu beschreiben. Das ist die Freie Enthalpie (Symbol G).
Alle drei Zustandsgrößen werden zu einer Zustandsfunktion, der Gibbs-Helmholtz-Gleichung, zusammengefasst.
ΔG = ΔH - T · ΔS
Das Minuszeichen drückt das Gegeneinanderwirken von Enthalpie und Entropie aus. Das Differenzsymbol Δ beschreibt die Änderung der Zustandsgrößen ausgehend vom Zustand vor der Änderung und danach. T ist die absolute Temperatur (in unserem Fall die Siedetemperatur).
Im ersten Fall sind ΔH und ΔS positiv.
ΔG = ΔH - T · ΔS
Im zweiten Fall ist das umgekehrt: ΔH und ΔS sind negativ.
ΔG = (-ΔH) - T · (-ΔS)
Eine Reaktion läuft so lange selbständig ab, wie die Änderung der Freien Enthalpie negativ ist, d. h., wie dem System Freie Enthalpie entzogen werden kann (negatives Vorzeichen von ΔG). Wenn die Änderung der freien Enthalpie gleich Null ist, kommt die Reaktion zum Stillstand; ein Gleichgewicht stellt sich ein. Muss ständig Freie Enthalpie zugeführt werden (ΔG hat dann ein positives Vorzeichen), so laufen die Vorgänge im System nicht mehr selbständig ab oder die Reaktionsrichtung kehrt sich um.
ΔG < 0 selbständig ablaufende Reaktion
ΔG = 0 Reaktion im Gleichgewicht, keine Änderung des Systems
ΔG > 0 Reaktion verläuft (wenn überhaupt) nur unter äußerer Einwirkung
in die Gegenrichtung
Beim siedenden Wasser gilt am Siedepunkt für ein Mol:
Verdampfungsenthalpie ΔH = 40,67 kJ/mol
Verdampfungsentropie ΔS = 0,109 kJ/mol · K
Absolute Siedetemperatur T = 373,16 K
Daraus berechnen wir mit der Gleichung von Gibbs und Helmholtz:
Freie Enthalpie ΔG = 40,67 - 373,16 · 0,109 = 0
Wir können das aber auch für den Abkühlvorgang berechnen:
Freie Enthalpie ΔG = (-40,67) - 373,16 · (-0,109) = 0
Das heißt, beim Sieden ist das System im Gleichgewicht. Der Vorgang läuft nicht selbständig ab, solange dem System nicht Wärme zu- oder abgeführt wird.
Der Einfluss der Umgebungstemperatur auf die Freie Enthalpie
Das klassische Beispiel für den Zusammenhang zwischen Temperatur und Reaktionsablauf ist die
Wassersynthese.
2 H2 + O2 ———> 2 H2O (fl.) + Energie
Es gibt auch eine thermische Wasserzersetzung:
2 H2O (fl.) + Energie ———> 2 H2 + O2
Letztlich können wir das als Gleichgewicht formulieren:
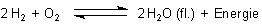
Ob nun Synthese oder Zersetzung im Vordergrund stehen, ist eine Frage der Umgebungstemperatur. Das können wir mit Hilfe des Gibbs-Helmholtzschen Satzes herleiten.
Für die Wassersynthese aus den Elementen ist ΔH stark negativ: ΔH = -286 kJ / Mol Wasser (Standard-Bildungsenthalpie). Da im System die Ordnung zunimmt, ist auch ΔS negativ: ΔS = -0,070 kJ / Mol Wasser (Standard-Bildungsentropie). ΔS ist allerdings vom Betrag her wesentlich kleiner als ΔH.
Setzen wir diese Werte in die Gibbs-Helmholtz-Gleichung ein, stellen wir fest, dass Größe und Vorzeichen von ΔG von der Temperatur abhängen:
| - | Bei nicht zu hoher Temperatur erhalten wir ein negatives ΔG. |
Wird die Temperatur gesteigert, so wird der insgesamt positive Ausdruck (-T · (-ΔS)) größer.
| - | Bei einer bestimmten Temperatur wird ΔG = 0. |
| - | Bei weiterer Steigerung von T kann der Ausdruck (-T · (-ΔS)) größer als ΔH werden. Dann wird ΔG positiv. Die Reaktion verläuft jetzt in die Gegenrichtung, also vorrangig auf Zersetzung. |
Die Temperatur, bei der ΔG gleich Null ist, kann man aus der Gibbs-Helmholtz-Gleichung berechnen.
0 = -286 · (T · (-0,07))
T = 4086 K
Die thermische Wasserzersetzung ist bei der Feuerwehr bekannt: Solche Temperaturen erreichen Metallbrände. Will man die mit Wasser löschen, so zersetzt sich das Wasser zum großen Teil; das entstehende Knallgas führt zu Explosionen und Verschlimmerung des Brandes. Solche Brände löscht man mit Sand oder besser noch mit trockenem Zement.
Weitere Texte zum Thema „Energie und Chemie“