Selbstgebasteltes C₆₀-Modell, mit dem ausführlich gearbeitet wurde
(Foto: Blume)

Die Struktur der Fullerene sowie deren Symmetrieelemente lassen sich gut mit Hilfe von einfachen Modellen erläutern. Diese können aus Papier, besser noch aus dünner Pappe oder Zeichenkarton hergestellt werden.

Bei der hier beschriebenen Methode erhält man Modelle, in denen die Fünfecksflächen offen sind. Damit wird das Zusammenkleben dieses Modells gegenüber vollständig geschlossenen Modellen erleichtert. Darüber hinaus lernen die Schüler hier bereits konkret beim Zusammenbau die Bedeutung der Fünfecke für die Struktur der Fullerene kennen ("learning by doing").

In den Bildern 1 und 2 sind ebene Netze aus Sechsecken für Modelle des C₆₀ und des C₇₀ dargestellt. Diese können als Kopiervorlagen verwendet werden. Falls möglich sollten Vergrößerungen auf DIN A3 - Papier angefertigt werden. Man kann sich aber auch mit Hilfe einer Sechsecksschablone Netze mit größeren Sechsecken herstellen.

Schritt 1:	Das Netz aus Sechsecken wird ausgeschnitten.
Schritt 2:	Entlang der mit Pfeilen gekennzeichneten Kanten wird das Netz eingeschnitten.
Schritt 3:	Die schraffierten Sechsecke werden ausgeschnitten.
Schritt 4:	Die Sechsecke mit gleicher Nummerierung werden übereinander gehalten oder geklebt. Dabei reduzieren sich die zunächst sechseckigen Löcher zu Fünfecken.

Legt man das Netz aus Sechsecken vor dem Ein- bzw. Ausschneiden an den Querkanten übereinander (Sechseck Nr. 9 auf Nr. 5 und Nr. 11 auf Nr.1), so erhält man ein röhrenförmiges Gebilde. Dies ist ein Modell für die Struktur eines "Buckytubes". Erst durch "Einfügen" der Fünfecke kann sich eine geschlossene Sphäre bilden.

Die Bedeutung der Fünfecke zur Bildung der geschlossenen, kugelförmigen Strukturen der Fullerene kann konkret in einem einfachen Teilmodell demonstriert werden. Hierzu schneidet man ein aus sieben gleichseitigen Sechsecken bestehendes Netzwerk aus (Bild 3). Es ist nicht möglich, ohne die Sechsecke in sich zu knicken, diese ebene Figur in die dritte Dimension zu krümmen.

Schneidet man dagegen das Netz entlang der mit einem Pfeil gekennzeichneten Kante ein und trennt das zentrale Sechseck heraus, so erhält man einen Teil der Fullerenstrukturen wie in den obigen Modellen. Klebt man nun die beiden mit K gekennzeichneten Sechsecke aufeinander, so entsteht aus dem mittleren Sechseck ein Fünfeck. Die vorher ebene Figur krümmt sich in den Raum hinein.

Literatur:

J. M. Beaton, "A Paper-Pattern System for the Construction of Fullerene Molecular Models", J. Chem. Educ. 69 (1992) 610 - 612.

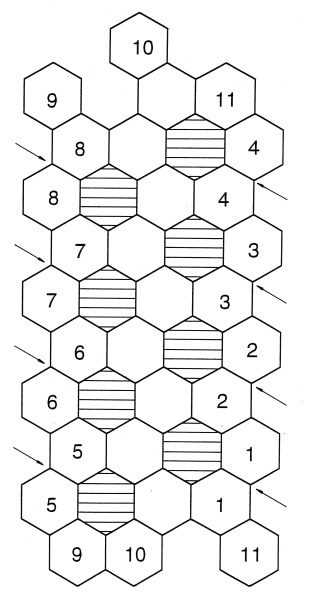
Bild 1: Vorlage für ein Modell des C₆₀

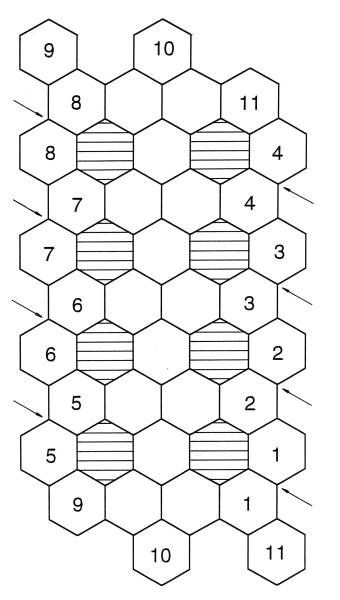
Bild 2: Vorlage für ein Modell des C₇₀

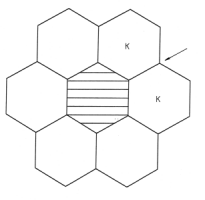
Bild 3: Modell zur Demonstration der Auswirkung des Einschiebens von Fünfecken in Netzen von regelmäßigen Sechsecken

Weitere Texte zum Thema „Fullerene“