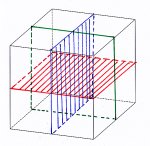
Die Symmetrie-Ebenen des kubischen Systems
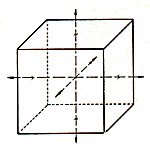
Zeichne einen Würfel (Kubus). In diesen zeichnest du die Symmetrie-Ebenen ein. Zunächst verbindest du dazu die gegenüberliegenden Seitenhalbierungspunkte. So erhältst du schon einmal drei Ebenen, die den Würfel spiegelsymmetrisch teilen.

Dann zeichnest du auf jeweils drei Seiten die Diagonalen, die du mit den gegenüberliegenden Seiten verbindest. Damit entstehen weitere sechs Ebenen.
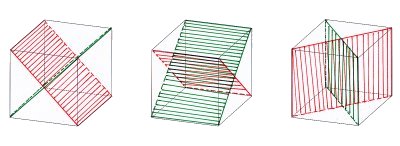
Mehr als diese neun Ebenen gibt es nicht. Trotzdem ist damit das kubische (oder reguläre) Kristallsystem das mit der höchsten Symmetrie.
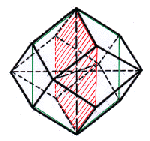
Das Rhombendodekaeder besteht aus 12 identischen Rhomben (Rauten), ist also sehr gleichförmig aufgebaut. Es hat 7 Symmetrie-Ebenen.
 |
 |
 |
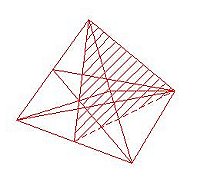
Beim Tetraeder kannst du nur sechs Symmetrie-Ebenen aus den Seitenhalbierenden von drei Dreiecksseiten konstruieren. Die erste Seite ergibt drei, die zweite Seite zwei Ebenen und die dritte nur noch eine Ebene. Die vierte Tetraeder-Fläche wird von den anderen drei "mit bedient".
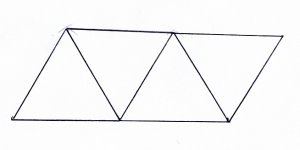
Am besten baust du dir ein Tetraeder. Das geht sehr einfach. Du musst nur das folgende Bildchen ausschneiden und entsprechend falten und zusammenkleben.
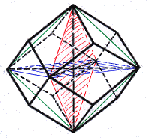
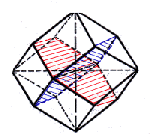
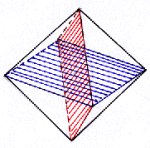
Beim Oktaeder findest du dagegen nur fünf Ebenen. Die sechs Oktaederspitzen sind zugleich die Mittelpunkte der sechs Würfelflächen.
 |
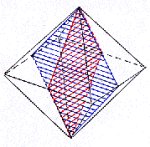 |
| Symmetrie-Ebenen des Oktaeders: links drei Ebenen, rechts zwei Ebenen |
Beim Pentagondodekaeder findest du nur noch drei Symmetrie-Ebenen.
Erst wenn man die kubischen Körper in einen Würfel stellt, so erhält man wieder alle 9 Ebenen - aber nur, wenn man den resultierenden Würfel auf Symmetrie hin untersucht.
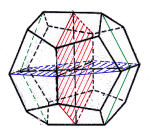
Entscheidend für das reguläre System ist also nicht die Zahl 9 der Symmetrie-Ebenen, sondern das Vorliegen von drei vierzähligen Drehspiegelachsen, die senkrecht aufeinander stehen.
Weitere Texte zum Thema „Kristalle“