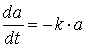
Herleitung des Konzentrations/Zeit-Gesetzes für A -> B
Das Geschwindigkeitsgesetz für diese Reaktion 1. Ordnung ist
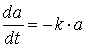
Umstellung zur Variablentrennung
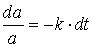
Integration
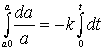
Ergebnis der unbestimmten Integration
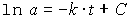
Mit den Integrationsgrenzen erhält man eine Form des Konzentrations/Zeit-Gesetzes für den Abbau von A
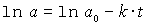
Trägt man ln a gegen t auf, so erhält man eine fallende Gerade. Die Steigung ist -k, der Ordinatenabschnitt ln ao.
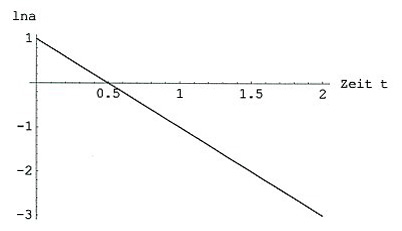
ln a als Funktion der Zeit für Reaktionen 1. Ordnung
Mit dieser Linearisierung kann man zugleich nachprüfen, ob die Reaktion tatsächlich dem Typ A -> B folgt.
Umstellung der Gleichung und Delogarithmieren führen zum endgültigen
Konzentrations/Zeit-Gesetz für das Edukt A
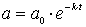
Dieses Gesetz gestattet, beim jeweiligen Zeitpunkt die verbleibende Konzentration von A zu berechnen.
Kontrollrechnungen
| t = 0 | a = a0 |
| t —> ¥ | a —> 0 |
Trägt man a gegen t auf, so erhält man eine Abklingfunktion.
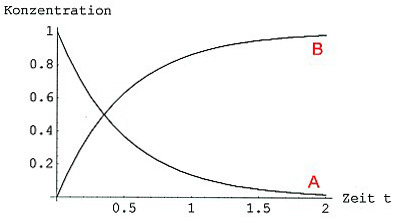
Konzentrations/Zeit-Kurven der Reaktion A —> B
Zur Herleitung des Konzentrations/Zeitgesetzes für die Bildung des Produkts B ist die
Konzentrations-Randbedingung
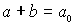
oder
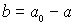
Einsetzen in das Konzentrations/Zeit-Gesetz des Edukts A
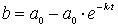
Ausklammern ergibt das gesuchte Konzentrations/Zeitgesetz für die Bildung des Produkts
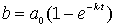
Dieses Gesetz gestattet, beim jeweiligen Zeitpunkt die Konzentration von entstandenem B zu berechnen.
Kontrollrechnungen
| t = 0 | b = 0 |
| t —> ¥ | b —> a0 |
Trägt man b gegen t auf, so erhält man eine Sättigungskurve, die zur Kurve für A spiegelbildlich verläuft (siehe Bild oben).
Berechnung der Halbwertszeit
Bedingung a = ao/2 einsetzen in Konzentrations/Zeit-Gesetz
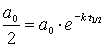
Kürzen und Kehrwert bilden
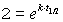
Logarithmieren und umstellen führt zu
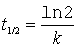
Die Halbwertszeit ist unabhängig von der Anfangskonzentration. Zum Lernen ist folgende Gleichung bestens geeignet.
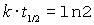
Weitere Texte zum Thema „Reaktionskinetik“