 |
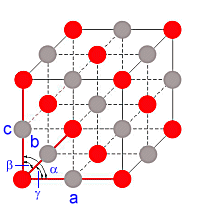
| Bild 1: Blick in das Kristallgitter von Natriumchlorid
(Zeichnung: Wolfgang) |
Die Elementarzelle
Zur Herleitung der Gesetzmäßigkeiten in Symmetrie und Aufbau von Kristallen betrachten wir noch einmal das Gitter eines Kristalls.
 |
| Bild 1: Blick in das Kristallgitter von Natriumchlorid
(Zeichnung: Wolfgang) |
Das Kristallgitter von Natriumchlorid besteht aus Natrium- und Chlorid-Ionen. Um es
quantitativ zu beschreiben, legt man ein dreidimensionales Koordinatensystem in den Eckpunkt
des Gitters. Dieses definiert sich durch drei Achsenabschnitte und drei Winkel.
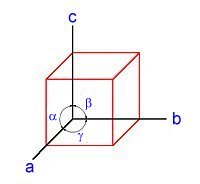 |
| Bild 2: Das allgemeine Koordinatensystem von Elementarzellen
(Zeichnung: Wolfgang) |
Der Abstand zwischen zwei identischen Punkten, also jeweils zwischen zwei Kationen oder
Anionen in vergleichbarer Lage, heißt Identitätsperiode. Man
nennt sie auch Gitterkonstanten. Davon gibt es drei:
a, b, c.
Diese schließen drei für jeden Stoff bzw. für jede Kristallart und bei
verschiedenen Modifikationen eines Stoffes charakteristische Winkel
ein: a, ß, g.
Ergänzt man die Achsenabschnitte zu einem Prisma, so
erhält man die Elementarzelle. Sie hat die
Symmetrie-Eigenschaften des ganzen Kristalls und definiert sein Kristallsystem. Das
Prisma kann je nach Winkel ausgesprochen schief aussehen. Im Falle des NaCl-Kristalls
besteht die Elementarzelle aus 4 Na- und aus 4 Cl-Ionen.
Die Symmetrie der Elementarzellen
Die Symmetrie eines Körpers erhält man, indem man Ebenen sucht, die den Körper
in zwei spiegelbildlich gleiche Hälften aufteilt. Diese Flächen nennen wir
Symmetrie-Ebenen. Beim Suchen nach Symmetrie-Ebenen
darf die Elementarzelle nicht gedreht werden, sondern muss immer von einer Seite, Kante oder Ecke
her betrachtet werden.
Eine andere Symmetrie-Operation ist die Ermittlung der Zähligkeit von Drehspiegelachsen. Durch Drehung um diese Achse kann man feststellen, wie oft im Laufe einer Drehung um 360 ° gleiche Flächen bzw. Flächenkombinationen auftreten: Wenn dies nach einer Drehung von 180 ° der Fall ist, spricht man von einer zweizähligen Achse (rhombisch, monoklin), bei einer Drehung um 120 ° von einer dreizähligen (trigonal), um 90 ° von einer vierzähligen (kubisch, tetragonal) und schließlich bei einer Drehung um 60 ° von einer sechszähligen Achse (hexagonal). Z. B. hat der kubische Würfel drei vierzählige Drehspiegelachsen, die dazu noch rechtwinklig aufeinander stehen.
Merkwürdig ist das Fehlen der fünfzähligen Symmetrie, also eines "pentagonalen" Systems. Es gibt auch keine siebenzähligen Achsen. Das gilt auch für "oktagonale" Systeme. Deshalb gibt es keine achteckigen Schneesterne.
Weitere Texte zum Thema „Kristalle“