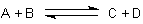
Die thermodynamische Begründung des
Massenwirkungsgesetzes und ΔG
Das Massenwirkungsgesetz wurde zuerst reaktionskinetisch begründet.
Dabei ging es vorrangig um die Dynamik der Einstellung des
Gleichgewichts und die Dynamik der Reaktionen zwischen den sich im Gleichgewicht
befindlichen Stoffen.
Dagegen vergleicht man bei der thermodynamischen Herleitung des
Massenwirkungsgesetzes die Grenzzustände des Gleichgewichtssystems bzw. die
Energien dieser Zustände am Ende der Rückreaktion und am Ende der Hinreaktion.
Wir nehmen folgendes Gleichgewicht an.
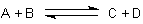
Am besten beschreiben wir die energetischen Zusammenhänge mit einer Größe, die den ersten und den zweiten Hauptsatz der Thermodynamik verbindet, der Freien Enthalpie ΔG.
ΔG ist ein Maß für das, was wir die "chemische Affinität" bezeichnen. Je größer sein
negativer Wert ist, desto mehr Arbeit vermag ein System zu leisten, desto reaktiver ist
es.
Es ist vernünftig, ΔG wie alle Potentialgrößen auf einen Zustand zu normieren. Dieser
Standardzustand liegt vor, wenn von allen beteiligten Stoffen in der
Reaktionsmischung jeweils 1 Mol vorliegt. Wir sprechen dann von ΔG0.
Es gibt eine einfache quantitative Beziehung zwischen der Freien Enthalpie unter Standardbedingungen, ΔG0, und der bei bestimmten Konzentrationen ci (bei Gasreaktionen: Partialdrücken pi) real verfügbaren Freien Enthalpie, ΔG.
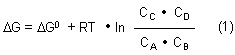
R ist die Gaskonstante, T die absolute Temperatur. Diese Gleichung entspricht
vollkommen der von Nernst! Das beruht auf der Proportionalität
der EMK und ΔG.
In dieser Gleichung bedeuten CA, CB (usw.) die Konzentrationen (genauer: Aktivitäten)
der Reaktionspartner A, B (usw.), die sich nicht im Gleichgewicht befinden. Deshalb
gilt die Gleichung (1) für beliebige Konzentrationen. Einige Besonderheiten wollen wir
herausarbeiten:
1 Sind unter Standardbedingungen alle Konzentrationen gleich 1 mol/l, so wird erwartungsgemäß ΔG = ΔG0.
2 Stellt sich ein Gleichgewichtszustand ein, so liegen alle Reaktanden in ihren Gleichgewichtskonzentrationen [A], [B] (usw.) vor. Damit wird der Konzentrationsquotient in der Gleichung (1) gleich Kc (bei Gasen Kp), der Gleichgewichtskonstanten.
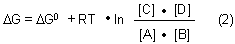
Gleichzeitig gilt für das chemische Gleichgewicht die fundamentale Beziehung
ΔG = 0 (3)
Denn ein System, das sich im Gleichgewicht befindet, leistet keine Arbeit mehr.
Mit beiden Bedingungen wird aus der Gleichung (2)
0 = ΔG0 + RT · ln K
ΔG0 = - RT · ln K (4)
Die Freie Enthalpie im Standardzustand kann somit aus der Gleichgewichtskonstante berechnet werden.
Ersetzen wir mit (4) in (1) den Ausdruck ΔG0, so folgt die allgemeine Beziehung für die Freie Enthalpie ΔG in einem beliebigen chemischen Reaktionssystem, das sich nicht im Gleichgewichtszustand befindet.
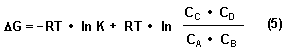
Die Gleichung (5) ist unter der Bezeichnung van´t Hoffsche Reaktionsisotherme bekannt. Der zweite Term mit dem Konzentrationsquotienten ist die so genannte Restreaktionsarbeit.
Reaktionen können nur dann spontan ablaufen, wenn ΔG < 0 ist, der Wert also negativ ist. Mit der Gleichung (5) können wir voraussagen, wie und in welche Richtungen Reaktionen ablaufen. Denn die Restreaktionsarbeit ist ein Maß für die Arbeits- bzw. Reaktionsfähigkeit eines Systems. Anders als den Term mit der Gleichgewichtskonstante können wir die Restreaktionsarbeit durch Konzentrationsveränderung variieren und damit den Wert und das Vorzeichen von ΔG und damit auch die Richtung der Gleichgewichtseinstellung beeinflussen.
Ist K < 1, so ist der Gleichgewichtsterm von vornherein positiv. Eine Reaktion kann in diesem Fall nur dann erzwungen werden, wenn die Konzentrationen im Term der Reaktionsarbeit so gewählt werden, dass ΔG insgesamt negativ bleibt. Das ist wichtig für Gleichgewichtsverschiebungen durch Konzentrationsänderung, einem der wichtigsten Aspekte des Le Chatelierschen Prinzips. Die Abhängigkeit von ΔG vom Konzentrationsquotienten der Restreaktionsarbeit kann man leicht berechnen. Ein Beispiel dazu bringen wir auf einer besonderen Webseite.
Ist die Restreaktionsarbeit gleich dem Term mit der Gleichgewichtskonstanten, wird in Gleichung (5) ΔG = 0; dann liegen die Reaktanden in ihren Gleichgewichtskonzentrationen vor. Der Konzentrationsquotient hat nun den Wert der Gleichgewichtskonstante. Damit hat sich ein nach außen hin reaktionsloser Gleichgewichtszustand eingestellt, aus dem heraus trotz aller Dynamik der Prozesse auf molekularer Ebene keine Reaktionsarbeit geleistet werden kann.
Industrielle und auch biologische Systeme müssen fern vom Gleichgewichtszustand arbeiten, denn ΔG = 0 bedeutet Reaktionsstillstand. Im Durchflussreaktor wie dem Hochofen läuft keine Reaktion mehr ab, und ein Organismus ist nach Stillstand des Fließgleichgewichts zum Sterben verurteilt.
Weitere Texte zum Thema „Chemisches Gleichgewicht und Massenwirkungsgesetz“