Ich will´s versuchen…
Chemiker denken beim Grübeln über chemische Reaktionen immer nur an Teilchen wie Atome, Moleküle, Ionen. Die sind aber verflucht klein. Deshalb bedienen wir uns des Molbegriffs. Ein Mol ist nichts anderes als eine Portion von 6 · 10²³ Teilchen. Das ist die Zahl der Atome, die in einem Gramm Wasserstoff enthalten sind. Ein Mol Wasserstoffatome wiegt also ein Gramm - das ist die Atommasse von Wasserstoff. (Leider kann man hier nicht die Atommasse und Molmasse gleichsetzen, denn Wasserstoff kommt in der Natur nur als Molekül vor, das aus zwei Atomen zusammengesetzt ist: H₂; deshalb ist die Molmasse also 2. Das soll hier aber im Moment nicht interessieren.) Die Atome der anderen Elemente sind schwerer, ein Kohlenstoffatom zum Beispiel ist 12mal so schwer als das vom Wasserstoff. Deshalb wiegen 6 · 10²³ (also ein Mol) Kohlenstoffatome eben 12 g.
Alles klar?

Und zu Recht fragt sich jeder Schüler und jede Schülerin, wie man denn die Molmassen überhaupt ermittelt. Deshalb geht es heute um Möglichkeiten zur Molmassenbestimmung. Weil es so am einfachsten geht, zeigen wir das am Beispiel von einigen Gasen.

Der italienische Physiker Amadeo Avogadro hat um 1830 nur durch Nachdenken herausgebracht, dass sich alle Gase gleich verhalten müssen. Dazu musste er sich nur darüber klar sein, das Gase aus kleinen Teilchen (Atomen und Molekülen) bestehen. Er meinte: In ein bestimmtes Volumen passt immer die gleiche Stoffportion von verschiedenen Gasen, egal ob die Gase aus großen oder kleinen Molekülen bestehen. Denn zwischen den Gasmolekülen ist ausreichend Platz, so dass der kleine Größenunterschied nicht weiter auffällt. Er hatte mit diesem Modell Recht.
Unter dem Begriff „Stoffportion" verstehen wir heute eine bestimmte Anzahl von Teilchen (Atome bei Edelgasen, Moleküle bei anderen Elementen wie Sauerstoff O₂, Stickstoff N₂ oder Verbindungen wie Kohlenstoffdioxid CO₂ oder Ammoniak NH₃). Wir nennen die Stoffportion von 6 · 10²³ Teilchen ein Mol.
Avogadro fand weiter heraus: Das Volumen von 1 Mol eines Gases beträgt bei 0 °C (273,16 K) und 1,013 bar Druck 22,4 l. Merken wir uns auch: Bei schnuckeligen 20 °C Raumtemperatur (abgekürzt RT) sind das 24,00 l/mol.
Für Kenner: Zur Umrechnung von Gasvolumen auf eine andere Temperatur nutzen wir die folgende Formel.

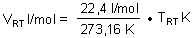
Die Gleichung folgt aus dem Zustandsgesetz für ideale Gase. Man nennt es merkwürdigerweise auch „Ideales Gasgesetz".

Wir müssen hier aber eine für die Praxis bedeutsame Einschränkung machen: Das Gesetz von Avogadro gilt (wie gesagt) streng für sogenannt „ideale" Gase. Darunter versteht man Gase, deren Teilchen keine Wechselwirkung aufeinander ausüben. Das sind nur Gase im Zustand weit weg von ihrem Siedepunkt. Denn beim Sieden hängen die Teilchen noch zusammen - und das bedeutet schlicht ein geringeres Volumen. Reale Gase haben also ein geringeres Molvolumen.
Deshalb können wir zur Molmassenbestimmung z. B. nicht Brom Br₂ einsetzen. Das siedet erst bei 58,78 °C.
Beim Kohlenstoffdioxid CO₂ (Siede- bzw. Sublimationspunkt -78,5 °C) ist die Abweichung vom Idealgas und damit der Fehler bei der Molmassenbestimmung unter Einbeziehung von Avogadros Annahmen deutlich: Das Molvolumen von CO₂ ist statt 22,4 nur 22,25 l/Mol bei 0 °C, bei 20 °C 23,88 l/Mol. Deshalb ist der Wert für die Molmasse von CO₂, die wir nach den unten folgenden Gleichungen berechnen, immer zu hoch, wenn wir die Molvolumina für ideale Gase einsetzen. Die Abweichung liegt unter 1 %, was die Aussage des Versuches nicht weiter stört.
Übrigens können wir im Unterricht umgekehrt die Abweichung vom Idealwert nutzen, um über die Eigenschaften eines realen Gases wie CO₂ zu sprechen.

Und noch etwas: Die im Folgenden beschriebenen Versuche lassen sich nicht bei Gasen anwenden, die leichter als Luft sind. Schon beim Stickstoff N₂ (besonders aber beim Wasserstoff H₂) muss die Messanzeige der Waage aufwendig auftriebskorrigiert werden. Denn das Gefäß mit dem leichten Gas strebt wie ein Luftballon noch oben, und die Waage zeigt deshalb einen zu geringen Wert an.

Nach dieser Vorrede kommen jetzt die Versuche. Die sind eigentlich erstaunlich einfach und machen erfahrungsgemäß Spaß.

Wir benötigen an Geräten:
Einen Erlenmeyerkolben (500 ml) mit Gummistopfen oder eine Gasmaus, Feinwaage (auf 2 Stellen genau), Grobwaage (grammgenau) oder Messzylinder (250 ml), Thermometer.

Gasmaus (Foto: Daggi)

Versuch 1: Bestimmung der Molmasse von wasserunlöslichen Gasen Vorbemerkung: Es dürfen keine wasserlöslichen Gase wie SO2, CO2, NH3 etc. eingesetzt werden. Wir nehmen auch keine Gase, die leichter sind als Luft. Aus einer zuvor genau abgewogenen kleinen Gasflasche (Gasfeuerzeug) lässt man über Wasser ein bestimmtes Volumen (etwa 1 - 2 l) Gas in einen großen Messzylinder ab. Das Volumen des abgelassenen Gases muss notiert werden. Da es sich beim Ablassen abkühlt, lohnt es sich, zur Temperierung etwas mit der Ablesung zu warten. In der Zwischenzeit trocknet man die Gasflasche gut (!) ab und wiegt erneut. Die Wägedifferenz ist die Masse des abgelassenen Gases.

Zur Berechnung der Molmasse formulieren wir einen Dreisatz:

Molmasse des Gases (g/mol) / Molvolumen (l/mol) (bei RT) = Gasmasse (g) / Volumen des abgelassenen Gases (l)

Daraus folgt für die Molmasse des Gases:

Hier sind unsere Messergebnisse:
500 ml wiegen 1,3 g. Das ergibt eine Molmasse von 62,5 g/mol. Es handelt sich um Butan (genaue Molmasse 58 g/mol). Die Abweichung ergibt sich daraus, dass Butan ein "sehr reales" Gas ist, das Molvolumen also kleiner ist als 24 l.

Versuch 2: Bestimmung der Molmasse von wasserlöslichen Gasen Vorbemerkung: Es können nur trockene Gase untersucht werden, die schwerer sind als Luft, also CO, CO2, O2, SO2. Ein Erlenmeyerkolben wird mit Gummistopfen gewogen. Nun wird das zu bestimmende Gas eingefüllt, der Kolben verschlossen und erneut gewogen. Anschließend wird das Volumen bestimmt, indem man den Kolben mit Wasser füllt. Entweder wird der Kolben mit einem Messzylinder gefüllt oder die einzufüllende Wassermenge durch Differenzwägung auf einer groben Waage bestimmt (1 ml Wasser = 1 g).

Was beim Wiegen des leeren Glases immer vergessen wird: Wir haben ja von vornherein ein Gas im Glas. Das ist die Luft. Deren Masse müssen wir bei der Bestimmung der Masse des wirklich leeren, also luftleeren Glases natürlich abziehen.

Masse des luftleeren Glases (g) = gewogene Glasmasse (g) - Volumen des Glases (l) · Dichte der Luft (g/l)

Die Dichte der Luft ist bei RT und 1,013 bar = 1,2 g/l.

Nun können wir die Gasmasse berechnen.

Gasmasse (g) = Masse des vollen Glases (g) - Masse des luftleeren Glases (g)

Die Molmasse wird dann wie im Anschluss zu Versuch 1 berechnet.

Hier sind unsere Messergebnisse:
Volumen 372 ml. Masse des Glases (mit Luft) 192,99 g, mit CO₂ 193,21 g. Die Molmasse berechnet sich zu 43,2 g/mol (Richtiger Wert 44 g/mol).

Rüdiger Blume

Weitere Tipps des Monats