Beim Experimentieren den Allgemeinen Warnhinweis unbedingt beachten.

Ein Experiment für kalte Jahreszeiten: Bei der Neutralisationsreaktion wird die chemische Reaktionsenergie in der Form von Wärme freigesetzt.

H⁺(aq) + OH^-(aq) ———> H₂O    /exotherm

Diese Energieumwandlung können wir im Chemieunterricht vielfach ausnutzen.

1 Endpunktsbestimmung bei Titrationen
Titriert man eine Säure mit einer Lauge ohne Zusatz eines Indikators, so ist der einzige Hinweis, dass bei einer Neutralisation eine chemische Reaktion abläuft, die simultane Wärmeentwicklung. Diese findet aber nur so lange statt, wie die chemische Reaktion abläuft. Ist sie beendet, hört auch die Wärmefreisetzung auf. Verfolgen wir deshalb die Temperatur beim Titrieren, sollten wir daraus den Endpunkt der Titration, also den Äquivalenzpunkt ermitteln können. Man bezeichnet das Verfahren treffend als Thermometrische Titration.

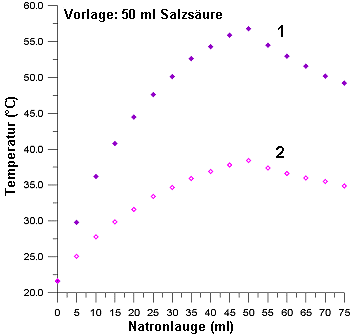
Bild 1: Thermometrische Titrationen von Salzsäure bei zwei verschiedenen Konzentrationen
(1 c = 5 mol/l; 2 c = 2,5 mol/l)

Das Abbiegen der ansteigenden Kurve resultiert aus der abkühlenden Wirkung der kalten Natronlauge. Nach dem Äquivalenzpunkt wird keine Wärme mehr frei, es wird durch die Laugenzugabe nur noch abgekühlt. Insgesamt resultiert ein Maximum.

Die Temperaturdifferenz ist proportional zur Konzentration der Lösungen. Dies kann mit anders konzentrierten Lösungen gezeigt werden. Wir wiederholen dazu die Titration, indem wir mit 2,5-molaren Lösungen arbeiten. Die obige Graphik bestätigt unsere Annahme. Dies ist auch ein schönes Beispiel für die Additivität von Wärmen. Es handelt sich bei der Neutralisationswärme also um eine kolligative Eigenschaft, also um eine Eigenschaft, die von der Menge der beteiligten Teilchen abhängt.

2 Berechnung der Neutralisationswärme
Mit den Daten aus der thermometrischen Titration lässt sich zumindest näherungsweise die Neutralisationswärme ermitteln.
Eine beliebige Wärme berechnet man nach der folgenden Formel:

Q = m · c · DT

Die Wärmekapazität c ist eine Stoffkonstante; für Wasser ist ihr Wert c = 4,186 J/g Grad. (Früher definierte man c als eine Kalorie/g Grad.) Wir nehmen vereinfachend an, dass die Wärmekapazitäten der Elektrolytlösungen gleich groß sind wie die von Wasser. (Real sind sie etwas kleiner.)

Mit DT = 56,8 - 21,6 = 35,2 °C und m = 100 g   folgt

Q = 100 g · 4,186 J/g Grad · 35,2 Grad

Q = 14,73 kJ

Die Molzahl der Säure in den vorgelegten 50 ml beträgt n = 5 mol · 50 ml/1000 ml = 0,25 mol. Bei der Titration dieser Säureportion entwickeln sich also 14,73 kJ an Wärme. Die molare Neutralisationswärme ist folglich die vierfache Menge:

DH =  - 58,9 kJ/mol

(Der Literaturwert beträgt  - 55,87 kJ/mol.)

3 Bestimmung der Dissoziationsenergien schwacher Säuren
Bekanntlich sind schwache Säuren dadurch charakterisiert, dass sie nur unvollständig dissoziiert sind. Die Dissoziation erfordert zusätzliche Energie. Titriert man deshalb eine schwache Säure, so erhält man eine niedrigere Neutralisationswärme als bei einer starken Säure wie der Salzsäure.
Ein konkretes Beispiel: Bei der Titration von reiner Blausäure (HCN) werden nur 12,2 kJ/mol frei, weil die Dissoziation der Blausäure in Protonen und Cyanid-Ionen 43,7 kJ/mol erfordert.
Wir wollen das am Beispiel der Essigsäure nachprüfen.

Die Neutralisationswärme von verdünnter Essigsäure erreicht nur 89 %, bezogen auf die der starken Salzsäure. Bei reiner Essigsäure ist der Anteil sogar nur noch 85 %. Daraus kann man die Dissoziationsenergie der Essigsäure berechnen.

DH_Diss (HAc) = DH_Neutral (reine HAc) - DH_Neutral (HCl)

DH_Diss (Hac) =  - 49,9 kJ/mol + 58,9 kJ/mol

DH_Diss (Hac) = 9 kJ/mol

Dieser Wert scheint, verglichen mit dem der Blausäure (43,7 kJ/mol), sehr klein zu sein. Das liegt aber daran, dass die Essigsäure in wässriger Lösung wesentlich stärker wirkt als die Blausäure und daher leichter dissoziiert. Das zeigen auch die pKs-Werte:

Essigsäure	4,75
Blausäure	8,68

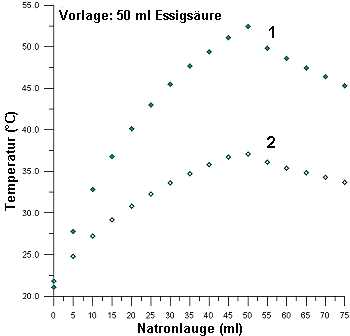
Bild 2: Thermometrische Titrationen von Essigsäure bei zwei verschiedenen Konzentrationen
(1 c = 5 mol/l; 2 c = 2,5 mol/l)

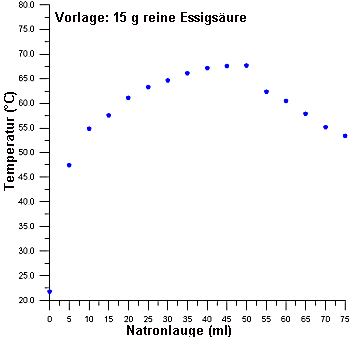
Bild 3: Thermometrische Titration von 0,25 Mol reiner Essigsäure mit Natronlauge (c = 5 mol/l)

Rüdiger Blume

Weitere Tipps des Monats