Bild 1: Sieben Eiswürfel sorgen garantiert für eine starke Abkühlung – beispielsweise von Rotwein
(Foto: Lüttgens)

Die m_Eisten Menschen entscheiden sicherlich spontan über die Zugabe von Eiswürfeln. Vielleicht auch, wie das Bild suggeriert, getreu nach dem Motto: Viel hilft viel. Mein Leistungskurs Chemie [*], der sich mit viel Engagement im letzten Semester mit thermodynamischen Überlegungen auseinandergesetzt hat, durfte sich auch dieser Aufgabe, einem praktischen Optimierproblem, intensiver annehmen. Heraus kam eine kleine Abschätzung, die ich hier präsentiere.

Ein einfacher Versuch
Zur Berechnung haben wir einige der bereits in anfangs erwähnten Tipp Formeln genutzt. Es lohnt sich also, dort nochmals nachzuschauen. Zuerst wird jedoch ein kleines Experiment durchgeführt. Dessen Ergebnis soll zur Bewertung der entwickelten Formel dienen.

Versuch 1: Schmelzen von Eiswürfeln - Messung der Temperatur Geräte und Chemikalien: Glas mit Leitungswasser, Eiswürfel aus dem Gefrierfach, Thermometer, Löffel zum Rühren Durchführung: Ein Glas wird mit Wasser gefüllt und die Temperatur TWasser gemessen. Anschließend werden unterschiedlich viele Eiswürfel hinzugegeben. Schließlich wird in regelmäßigen Zeitabständen oder nach dem vollständigen Schmelzen der Eiswürfel die Temperatur des Wassers möglichst mittig im Glas bestimmt. Beobachtungen: Der Wasserstrahl wird zum Ballon hin in seiner Fallrichtung abgelenkt. Bild 2: Messanordnung des Versuchs vor der Zugabe der Eiswürfel. Ein einfacher Versuch, der zu Hause durchgeführt werden kann. Hinweis: Während der Messung sollte ab und zu umgerührt werden, bevor die Temperatur bestimmt wird. (Foto: Lüttgens) Ergebnis: Je nach Anzahl der Eiswürfel kühlt sich das Getränk unterschiedlich rasch und unterschiedlich stark ab.

Der Versuch wurde mit 1, 3 und 7 Eiswürfeln (je ca. 18 ml Volumen) zur Abkühlung von 300 ml Wasser mit einer Anfangstemperatur von 20°C durchgeführt. Die Messung wurde entweder nach dem Schmelzen der Eiswürfel oder nach spätestens 12 Minuten beendet.

Bild 3: Links: Drei Eiswürfel, nach 10 Minuten vollständig geschmolzen, führen zu einer Temperatur von 7° C.
Rechts: Sieben Eiswürfel kühlen 300 ml Wasser auf 4° C ab.
(Foto: Lüttgens)

Gibt es eine einfache Formel?
Bevor wir versuchen, eine einfache Formel zur Berechnung, oder sagen wir besser: zur Voraussage der kühlenden Wirkung von unterschiedlich vielen Eiswürfeln in einem Kaltgetränk, aufzustellen, sind einige Annahmen zu treffen:

• Nur die Phasen, in denen sich die Eiswürfel aus dem -18°C kalten Eisfach im Wasser auf 0° C aufwärmen und anschließend schmelzen, sind für die Temperatur des Kaltgetränks relevant. Die 3. Phase der Mischung von 0° C kalten und 20° C warmem Wasser wird nicht berücksichtigt, da ihr Beitrag zur Energiebilanz zu vernachlässigen ist.
• Jegliche Abgabe von Wärme an die Umgebung über das Glasgefäß wird vernachlässigt. Wir gehen davon aus, dass das Glas mit Leitungswasser ein abgeschlossenes System darstellt.
• Der Zerteilungsgrad des Eises hat keinen Einfluss auf den Temperaturverlauf.

Was soll die Formel leisten? Schön wäre es, wenn man die Anzahl n der benötigten Eiswürfel leicht berechnen könnte, die notwendig sind. Dazu sollten die Angabe des Volumens V_Wasser und die gewünschte Abkühlung ΔT_Wasser des warmen Getränks genügen. Versuchen wir es mal...

Die Änderung der Temperatur des Wassers ΔT_Wasser ergibt sich aus der Temperaturänderung der Aufwärmphase des Eises auf 0° C ΔT_Aufwärm (1. Phase) und der Temperaturänderung der Schmelzphase ΔT_Schmelz bei 0° C (2. Phase):

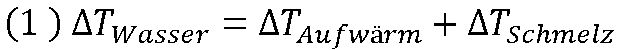
Für beide Temperaturänderungen haben wir bereits Formeln im angesprochenen Tipp genutzt. Die hier verwendeten Größen sind dort ebenfalls zu finden. Gehen wir nun schrittweise vor:

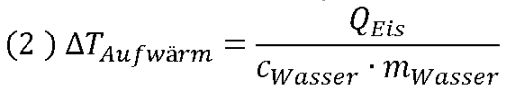
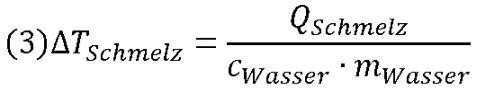
Mit Q_Schmelz = q_Schmelz · m_Eis ergibt sich aus (3):

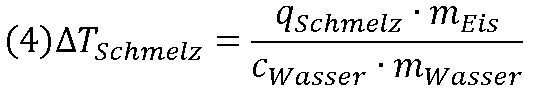
Setzen wir (2) und (3) in (1) ein, ergibt sich:

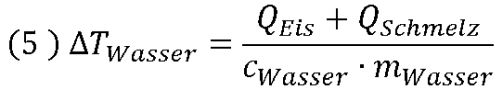
Nutzen wir nun noch die Formel für die Wärmeenergie des Eises Q_Eis = c_Eis · m_Eis · ΔT_Eis, sollten wir alles beisammenhaben, um die gewünschte Formel zu erstellen:

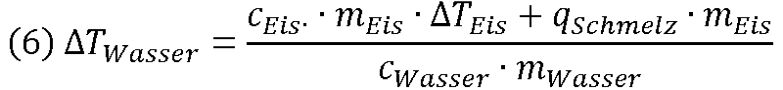
Vereinfacht ergibt sich:

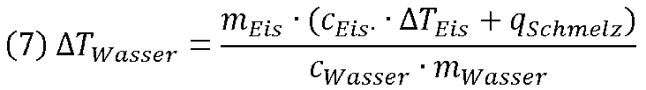
In dieser Formel finden sich alle für uns interessanten Informationen. Nun muss diese Formel noch so umgestellt werden, dass wir nur noch die Variablen eingeben brauchen, um die Masser der Eiswürfel m_Eis zu bestimmten:

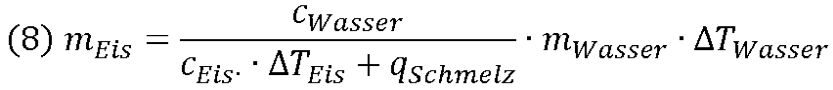
Oder einfacher, wenn das Eis aus dem Gefrierfach kommt und eine Temperatur T_Eis = -18 °C hat und somit ΔT_Eis = 18 K beträgt:

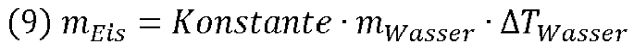
Berechnen wir nun die Konstante:

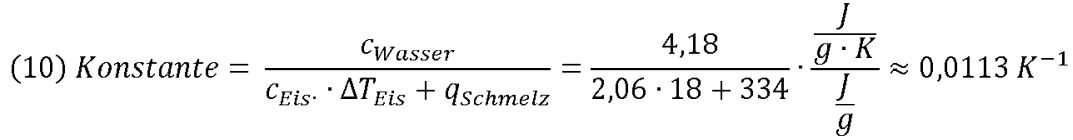
Nun haben wir eine einfache Formel gefunden, in die nur eingesetzt werden muss:

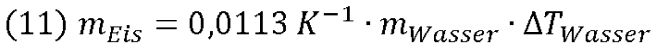
Testen wir unsere Formel...
Die für das oben beschriebene Experiment verwendeten Eiswürfel hatten ein Volumen von ca. 18 ml; wir gehen also von einer Masse für einen Eiswürfel von m_Eiswürfel = 18 g aus. Damit ergibt sich für die Anzahl der Eiswürfel:

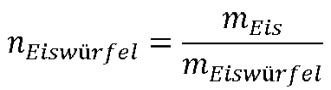
Gegeben ist weiterhin die Wassermasse m_Wasser = 300 g, das von 20° C auf 5° C abgekühlt werden sollen. Damit ist der Betrag von ΔT_Wasser = 15 K.

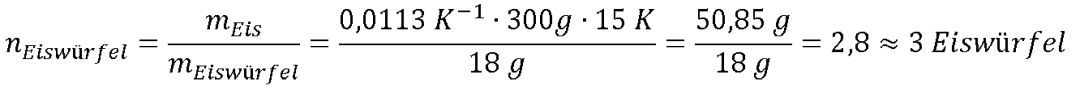
Ein Vergleich mit dem experimentellen Ergebnis, bei dem sich für ein Kaltgetränk von 300 ml drei Eiswürfel zu einer raschen Abkühlung auf 7° C ergeben haben, zeigt, dass unsere einfachen Annahmen vollkommen ausreichen, um ein zufriedenstellendes Ergebnis zu bekommen. Anders gesagt: Die Formel zu Lösung des Optimierproblems kann als tragfähig betrachtet werden, schließlich wird sie durch das Experiment annähernd bestätigt.

Zu guter Letzt...
Sollten Sie anhand der hier entwickelten Formel beim nächsten Besuch in einen Club den Barmixer in ein Gespräch über die optimale Anzahl an Eiswürfeln verwickeln wollen, während er ein cooles Getränk für Sie zubereitet, könnte es leicht passieren, dass Sie für eine physikochemischen Nerd gehalten werden. Wollen Sie das?

Noch eine Anmerkung von Professor Blume: Er kühlt seinen Rotwein (neben Spätburgunder - nach alter Tübinger Tradition - Lemberger-Trollinger) selbstverständlich ohne Eiswürfel, einfach im Kühlschrank. Schließlich sollte der kostbare Wein keinesfalls verwässert werden...

Referenzen:
[*] Mein Dank für die Berechnung des Optimierproblems für diesen Tipp des Monats gilt Clara Stockburger, Charlotte Wagener, Fabian Fritsch, Johannes Hengstmann und Fabian Plamper (Leistungskurs Chemie 2021/22 des Humboldt-Gymnasiums Berlin-Tegel).

Weitere Tipps des Monats