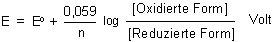
Für Spezialisten
Wovon hängt das Redoxpotential eines Bleiakkus ab?
Experimente:
Versuch: Messen des Potentials eines Blei-Akkus
Diese Frage stellte mir vor kurzem ein Schüler - wohl im Rahmen seiner Facharbeit: „Wovon
hängt das Redoxpotential eines Bleiakkus ab?“ Ich empfahl ihm: "Leiten Sie die Redoxgleichungen
her und stellen Sie für jede getrennt die Nernstsche Gleichung auf. Dann können Sie die
Potentialbedingungen aufstellen." Führen wir das einmal vor.
Zur Herleitung der Nernstschen Gleichung eine Vorbemerkung
Im Zähler des Konzentrationsquotienten (also "oben") stehen immer die Konzentrationsterme der
oxidierten Form. Dann ist das Vorzeichen des log-Terms ein Plus. Das besagt ja auch nichts anderes
als: Steigere die Konzentration des oxidierten Teils eines Redoxsystems, und das Potential wird steigen.
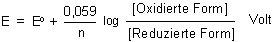
Im umgekehrten Fall ist das Vorzeichen des log-Terms ein Minus! Hier lautet die Botschaft: Steigere die Konzentration des reduzierten Teils eines Redoxsystems, und das Potential wird sinken.
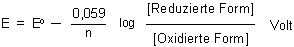
Die Anwendung der Nernstschen Gleichung auf den Bleiakku
Den Bleiakku und seine Potential-liefernden chemischen Reaktionen haben
wir schon beschrieben.

Im Folgenden untersuchen wir den Ladevorgang eines entladenen Akkus. Zum besseren Verständnis zerlegen wir diesen Redoxvorgang in seine zwei Elementarvorgänge Oxidation und Reduktion und leiten anschließend für beide getrennt die Nernst-Gleichungen ab. Anschließend berechnen wir durch Differenzbildung das Potential, das zwischen den beiden Elektrodenräumen herrscht.
Für besonders kluge Spezialisten:
In der Elektrochemie zählen Konzentrationen wenig…
Jetzt müssen wir noch etwas ausholen: Statt der Konzentrationen verwenden Wissenschaftler in der Elektrochemie
und der Thermodynamik im Allgemeinen eine Größe namens Aktivität. Darunter versteht man den Anteil der Teilchen,
die bei dem untersuchten Vorgang tatsächlich eine Rolle spielen – was nicht immer gleich der Konzentration ist.
Damit trägt man der Tatsache Rechnung, dass sich in Lösung befindliche, vor allem geladene Teilchen gegenseitig
beeinflussen. Sie können sich nicht frei bewegen und entziehen sich so dem normalen chemischen Reaktionsgeschehen
oder den Messungen.
Konkret: Wir haben ein gelöstes Salz mit der Konzentration 1 mol/l. Die Konzentration ist sehr hoch. Deshalb trennen sich die entgegengesetzt geladenen Teilchen nicht richtig voneinander. Nehmen wir an, das seien 70 % der jeweiligen Ionen (z. B. Na+ und Cl-). Dann ist die Aktivität 0,3.
Diese Aktivität schreiben wir nicht mit dem in der Schule üblichen Konzentrationssymbol wie beispielsweise c(PbSO4). Zur Unterscheidung schreibt man für die chemischen Aktivitäten ein anderes Symbol: a(PbSO4) oder meinetwegen auch [PbSO4]. Letzteres machen wir in dieser Webseite.
Die Aktivitäten a sind im Gegensatz zu den Konzentrationen c dimensionslos. Das wird verständlich, wenn man an Formeln denkt, in denen Aktivitäten eine Rolle spielen. Das sind häufig logarithmische Beziehungen, wie z. B. bei Gleichgewichtskonstanten oder bei der Definition des pH-Werts. Das geht bei einem Logarithmus auch gar nicht anders: Dieser leitet sich mathematisch aus einem dimensionslosen Verhältnis her. Bekanntlich gilt:
Integral (dn/n) = ln n
Im Allgemeinen kann man ab Konzentrationen kleiner als 10-2 mol/l molare Konzentrationen und Aktivitäten gleichsetzen.
Als ausführliches Beispiel beschreiben wir die Anwendung des Aktivitäten-Begriffs auf die Berechnung von pH-Werten klicke hier.
Bleibt noch die folgende Frage: Warum führen wir die Aktivitäten überhaupt ein? Verwirrt das nicht? Wir werden die Notwendigkeit gleich einsehen, wenn es um die Konzentrationen der Festkörper des Redoxsystems geht, um die so genannten „festen Phasen“.
1 Oxidation (Anode; ist beim Ladevorgang am Pluspol des Ladegeräts
angeschlossen)
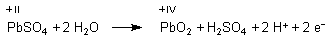
Mit der Nernstschen Gleichung berechnen wir das Potential der Anode.
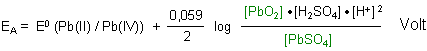
Die Aktivitäten von PbO2 und PbSO4 werden - da sie als Festkörper konzentrationsunabhängige Faktoren sind - üblicherweise gleich 1 gesetzt. (Denn es ist schließlich egal, ob unter einem Liter Lösung 10 g oder 100 g oder 1 kg Festkörper bzw. Bodensatz vorhanden sind; die Konzentration des daraus gelösten Stoffs ist immer gleich.) Aber auf keinen Fall darf man sagen, dass man die Konzentration gleich 1 mol/l setzt, weshalb man sie wegfallen lassen kann!
2 Reduktion (Kathode; ist beim Ladevorgang am Minuspol des Ladegeräts
angeschlossen)
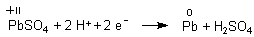
Mit der Nernstschen Gleichung berechnen wir das Potential der Kathode.
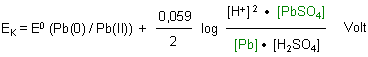
Die Aktivitäten von Pb und PbSO4 werden - da sie als Festkörper konzentrationsunabhängige Faktoren sind - wieder gleich 1 gesetzt.
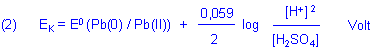
Nernstsche Gleichung für den gesamten Akkumulator
Dazu bilden wir die Differenz zwischen den Potentialgleichungen für die Anodenprozesse (1) und für die der Kathode (2).
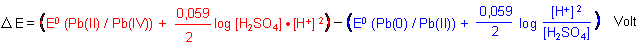
Daraus folgt diese erstaunlich einfache Beziehung:
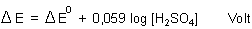
Die Potentialdifferenz eines Bleiakkumulators hängt also nur von der Konzentration (genau: Aktivität) der Schwefelsäure ab.
(Natürlich kommen noch andere potentialbestimmende Faktoren hinzu, wie z. B. die Auswirkung der Konzentration der Schwefelsäure auf die Aktivitäten sowie auf die Protolyse des Wassers. Hinzu kommt die Beeinflussung der Elektrodenoberflächen (usw.). Aber das sind technische Fragen, die wir hier nicht weiter vertiefen wollen.)
Weitere Texte zum Thema „Elektrochemie“