Experimente:
Versuch: Alkoholtest mit der Alkohol-Dehydrogenase (ADH)
Versuch: Reaktionskinetische Analyse der Urease-Reaktion

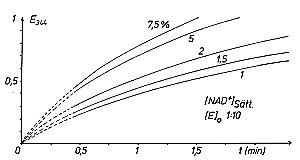
Wenn man Kinetiken von Enzymreaktionen aufnimmt, so erhält man primär die für reaktionskinetische Messungen bekannten Abkling- oder Sättigungskurven (-> Versuch) im c / t -Diagramm (Bild 1). Statt der Konzentration c kann man auch direkt zu c proportionale Größen wie die Absorption von VIS- bzw. UV-Strahlung (Extinktion) oder (im Falle von Leitfähigkeitsmessungen) den Leitwert auftragen (-> Versuch).

Bild 1: Eine Serie von Einzelmessungen zur Ermittlung der Anfangsgeschwindigkeit bei Enzym-Substrat-Reaktionen; Extinktions-Zeit-Kurven der ADH-Reaktion;
Parameter ist die relative Substratkonzentration (Ethanol) [1]

Diese Messungen auszuwerten ist sehr schwierig, weil sich während der Aufnahme der Messkurven die Reaktionsordnung ändert. Es erwies sich als praktikabel, die Anfangsgeschwindigkeit v₀ zu ermitteln und deren Abhängigkeit von der Substratkonzentration zu untersuchen. Erstere ist gleich der Steigung der c / t -Kurve im Startpunkt der Reaktion, also bei t = 0. Grund: Die Reaktion verläuft zu Beginn nicht nur am schnellsten, sondern ist auch noch unbeeinflusst von Rückreaktionen, Hemmung durch Produkte, Folge- und Nebenreaktionen (usw.).
Trägt man diese Anfangsgeschwindigkeit gegen die zugehörige Substratkonzentration auf, so erhält man gebogene Sättigungskurven wie in Bild 2.

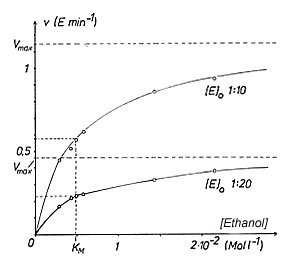
Bild 2: Geschwindigkeits/Substratkonzentrations-Diagramm einer Enzymreaktion;
Beispiel ADH mit zwei Enzymkonzentrationen [1]

Die Annahmen
Mit diesem Verhalten befassten sich L. Michaelis und M. Menten.
Hier sind ihre Überlegungen:
Die Sättigungskurven lassen sich dadurch erklären, dass das Enzym E sich mit seinem Substrat S zu einem Enzymsubstrat-Komplex ES verbindet. Es stellt sich ein schnelles Bildungsgleichgewicht ein. Dieser Komplex reagiert in einer langsamen Reaktion unter Rückbildung des Enzyms zum Produkt P. Damit ist die Produktbildung bestimmend für die Gesamtgeschwindigkeit (-> Folgereaktionen). Es ist eine Maximalgeschwindigkeit zu erwarten; dieser Sättigungszustand ist dann erreicht, wenn alle Bindungsstellen des Enzyms mit Substrat belegt sind. Sie ist also eine Frage der Substratkonzentration.

Briggs-Haldane erweitern den Ansatz von Michaelis-Menten
Michaelis und Menten nahmen an, dass die Geschwindigkeit der Produktbildung vernachlässigbar klein ist und deshalb ihre Konstante nur als eine Komplexbildungskonstante ("Substratkonstante K_s") formulierten. Wir gehen jedoch vom erweiterten Ansatz nach G. E. Briggs und J. B. S. Haldane (1925) aus und berücksichtigen in unseren Rechnungen auch die Geschwindigkeitskonstante der Produktbildung.

Die Herleitung der Michaelis-Menten-Gleichung
Die Ausgangslage ist also eine Reaktionskette mit vorgelagertem schnellem reversiblen Gleichgewicht. Da einer der Stoffe Katalysator ist, bildet er sich zurück. Statt einer Reaktionskette haben wir einen Katalysereaktionszyklus.

Zur Herleitung der Michaelis-Menten-Gleichung gehen wir aus Praktikabilitätsgründen von der linear formulierten Reaktionskette aus:

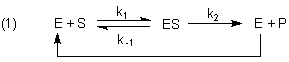
In den folgenden Gleichungen bedeuten

[E]	=	Konzentration des Enzyms zum betreffenden Zeitpunkt
[E]0	=	Gesamtkonzentration des Enzyms
[ES]	=	Konzentration des Enzymsubstratkomplexes zum betreffenden Zeitpunkt
[S]	=	Substratkonzentration zum betreffenden Zeitpunkt

Die Bildungsgeschwindigkeit von ES ist die einer Reaktion 2. Ordnung

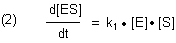
Außerdem wird ES durch zwei Reaktionen 1. Ordnung abgebaut, einmal durch die Rückreaktion im Sinne eines Komplexzerfalls und weiter durch die Produktbildung.

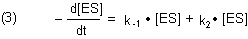
Im Gleichgewichtszustand ("Steady State") sind die beiden Geschwindigkeiten gleich:

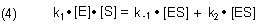
Die folgenden Rechnungen zielen darauf, die unbekannten Konzentrationen von ES und E in den Gleichungen zu isolieren, um sie zu Gunsten messbarer Größen zu eliminieren.

Wir fassen die rechte Seite in Gl. (4) zusammen, teilen durch k₁ und bekommen einen Ausdruck, in dem alle Geschwindigkeitskonstanten in einem Term zusammengefasst sind.

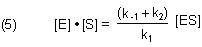
Der Konstanten-Term in (5) ist die berühmte Michaelis-Konstante K_M in der Form von Briggs-Haldane.

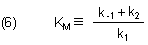
(Merkhilfe: Im Nenner steht die Geschwindigkeitskonstante der ES-Bildungsreaktion. Der Zähler ist die Summe der Konstanten der beiden ES-Zerfallsreaktionen.)

Man erkennt, dass K_M keine Gleichgewichtskonstante im Sinne einer Komplexbildung ist, sondern eine echte kinetische Konstante. Man kann sie zur Verdeutlichung "auseinandernehmen".

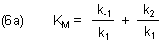
Hierbei ist der Quotient k_-1 / k₁ eine Gleichgewichtskonstante, die die Dissoziation eines Komplexes beschreibt. Michaelis und Menten nannten sie Substratkonstante K_s.

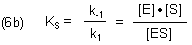
Der Term k₂ / k₁ beschreibt dagegen als kinetische Konstante eine lineare Folgereaktion des Typs A -> B -> C. Ist k₂ sehr klein im Vergleich zu k_-1, so haben wir den Michaelis-Menten-Fall mit K_M = K_s.

(5) und (6) ergeben zusammen

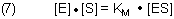
[ES] ist unbekannt. Mit der für die Kinetik üblichen stöchiometrischen Randbedingung [E]₀ = [E] + [ES] folgt aus (7)

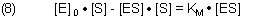
Wir lösen die Gleichung nach [ES] auf.

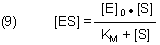
Die ebenfalls unbekannte Konzentration von E können wir durch folgende Überlegung eliminieren:
Die Geschwindigkeit der Gesamtreaktion, also die Produktbildung, hängt vom Zerfall von ES in Richtung auf die Produktbildung ab. Das Gesetz gilt nur, wenn es sich bei der Geschwindigkeit um die von Michaelis und Menten eingeführte Anfangsgeschwindigkeit v₀ der Enzymreaktion handelt.

(10)          v₀ = k₂ · [ES] ; daraus folgt: [ES] = v₀ / k₂

Wir setzen ES aus (10) in (9) ein und erhalten nach Umformung

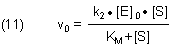
Der Ausdruck k₂ · [E]₀ ist die Maximalgeschwindigkeit V_max, d. h. diejenige Geschwindigkeit, die man erhält, wenn die gesamte Enzymmenge in der Form ES vorliegt. Das ist die Geschwindigkeit, bei der das Enzym unter Bedingungen der Vollsättigung arbeitet. Hier ist das Bildungsgleichgewicht des ES-Komplexes vollständig auf die Seite ES verschoben; [ES] = [E]₀. Nach dem Zerfall von ES zu E + P wird das freiwerdende aktive Zentrum augenblicklich wieder von Substratmolekülen besetzt. Dies wirkt sich aus, dass Produkt gebildet wird, ohne dass die Konzentration des Substrats merklich abnimmt. Man kennt dies von Reaktionen Nullter Ordnung, die auch von der heterogenen Katalyse her bekannt sind.

Mit (11) erhalten wir die endgültige Michaelis-Menten-Gleichung.

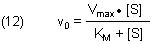
(Mathematisch betrachtet ist die Michaelis-Menten-Gleichung eine verschobene, rechtwinklige Hyperbel. Siehe hierzu unsere Webseite.) Wir erkennen anhand der Gleichung (12), dass die Michaelis-Konstante die Dimension einer Konzentration besitzt.

Bestimmung der Michaelis-Konstante
Die Michaelis-Konstante erhält man, wenn man in Gl (12) v₀ = V_max / 2 setzt. Dann folgt

(13)          [S]_halbsätt = K_M

Vergleiche hierzu Bild 2.

Die Michaelis-Konstante ist die Substratkonzentration bei Halbsättigung des Enzyms.

Aus einer gebogenen Kurve, die zudem häufig genug nicht zu Ende gemessen werden kann, ist es schwierig, die Halbsättigung zu ermitteln. Deshalb gab es schon früh Versuche, die Kurve zu linearisieren. Eine Methode ist die nach Lineweaver-Burk.

Zum Schluß ein Hinweis
Anfänger verwechseln die Kurve im Michaelis-Menten-Diagramm häufig mit der c / t -Sättigungskurve, die man zum Beispiel bei den Produkt-Kurven bei Reaktionen 1. Ordnung erhält. Man muss deshalb unbedingt darauf hinweisen, dass es sich beim Michaelis-Menten-Diagramm um ein aus c / t -Kurven hergeleitetes Sekundär-Diagramm handelt.

Literatur
[1] R. Blume, Quantitative Enzymkinetik: Die Alkoholdehydrogenase (ADH); 1. Charakteristik, kinetische Analyse und Substratspezifität; Praxis der Naturw. (Biologie) 27 (1978), 65-78.

Weitere Texte zum Thema „Reaktionskinetik“